Finding and Completing the Square
Let's step away from our yogurt problem real quick to a slightly different one with a little bit nicer numbers to make finding the pattern easier - say, (x + 5)2. Well, that's just (x + 5)(x + 5), which we can FOIL out to be x2 + 10x+ 25.
So what relationship do the numbers in the standard form expression have with each other? Well, it might be a little bit tricky to see, but it turns out that our b value, 10, divided by 2 (which is 5) and then squared turns into our c value, 25. Since we know that this trinomial can be factored into a perfect square binomial, (x + 5)2, it will turn out that any trinomial where the middle value divided by 2 and then squared is our final value, the c value, will be able to be factored as a perfect square binomial. If we want to say that same thing in math, we're looking for a trinomial with a c value that is equal to (b/2)2. If that's the case, it can be factored as a perfect square binomial.
So, in order to do this, we need our c value to be a specific number. But when we've got an equation that we can, say, add 20 to both sides of, we can make that c value whatever we want. This allows us to force the c value into being the exact number we need it to be in order to become a perfect square binomial. This process of changing the c value into the exact right number that makes it fit the pattern and become a perfect square binomial is what mathematicians call completing the square.
Yogurt Profit
Let's see how we would do this with our yogurt problem in order to determine the right number of toppings to offer. We were here - y = -x2 + 36x - 224 - but now we know that our c value needs to be something specific in order for it to work as a perfect square binomial. What it needs to be is the middle number, 36, divided by 2 (18) and squared (324). Right now our c value is -224, so it's not quite the right number. Our trinomial is not ready to be factored as a perfect square binomial... yet.
What we can do is use inverse operations on both sides of the equal sign to turn it into that number that we need, 324. Now, this is actually kind of a strange example and because we have this negative sign, a negative a value, we actually need our c value to be -324. So if I want the c value to be -324, and right now it's -224, I simply need to make it 100 smaller. That means we can subtract 100 from both sides of the equation, giving us this: y - 100 = -x2 + 36x - 324. Now that our c value is the exact right value that it needs to be, we can factor it into a perfect square binomial.
First let's take this negative sign out of everything, dividing that out, putting it in front and then changing the sign on everything else. And now we need to factor the trinomial on the inside of the parentheses, (x2 - 36x + 324). Finding two numbers that multiply to 324 and add up to -36 might be a little hard to find, but eventually we'd come to -18 and -18. The fact that they are both the same number and also equal to one half of 36 means that we're on the right track!
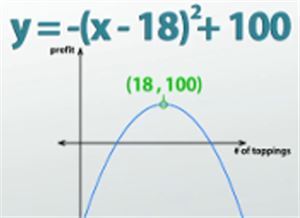
Once we've found those two numbers, we can factor the expression and rewrite it as this: y - 100 = -(x - 18)(x - 18), and then because they're both the same, we can combine them into one and change it into this: y - 100 = -(x - 18)2. We have now completed the square! We took a trinomial and turned it into a perfect square binomial. One last step to change it into vertex form means adding the -100 back over to the other side of the equation, and we now have our vertex form, y = -(x - 18)2 + 100. Remembering that the h and k values of vertex form tell us where the vertex is, the vertex of our parabola was at (18, 100). That means that 18 is the optimal number of toppings to sell, and I'll make $100,000 if I do that. Hmm, maybe I should rethink being a teacher...
Completing the square can be really hard to see at first, and it's probably one of the most complicated things you'll need to learn in an algebra class. Now that you know the general idea, it's probably a good bet to check out the later lesson where we'll focus on the process and do some practice problems.