GRE General: Functions Identification Notation
Inverse Functions

Inverse functions are two functions that do exactly opposite things. Check out this lesson to learn about how to write inverse functions, find inverse functions, and predict whether or not they exist.

Inverse Functions

f(x) =

\frac{x - 5}{2}

f^-1(x)=2x + 5

The second function is the inverse of the first one

You probably haven't had to watch very many of these videos to hear me say the words 'inverse operations.' I use this term to talk about how we can solve algebraic equations - maybe like this one: 2x + 3 = 9 - by undoing each number around the variable. For example, we undo a plus 3 with a minus 3 because addition and subtraction are inverse operations. We can then also undo a times by 2 with a divide by 2, again, because multiplication and division are inverse operations.

In just the same way, an inverse function is a function that is the opposite of another one. If a function is a set of steps to do to a number, its inverse is just a different set of steps that undoes everything the original function did.

For example, if we had one function f(x) that told us to start with a number, subtract 5, and then divide by 2, its inverse function would, instead, do all the opposite operations in the opposite order. That means that it would start with the same number, multiply it by 2 first, and then add 5.

Notice that we use this f to the -1 power notation to indicate an inverse function. This has to do with what an exponent of -1 means, but it's not really important that you understand why we use it, only that we do.

Confirming Inverses

f^-1(x)=2x + 5
f(f^-1(x)) =

\frac{2x + 5 - 5}{2}

Function composition is used to check inverse functions

Once we have a function and its inverse, we can check to make sure they are inverses by using function composition. If you're not familiar with this process, there is a video you can watch to learn about it, but basically it means plugging one function into another. The idea is that since inverse functions do the exact opposite things, if we compose them together, we should end up exactly where we started - just a plain x. Let's try this with our example above.

Substituting in f ^-1 into f means evaluating f(f^-1(x)). Plugging an f inverse function wherever we used to see an x in the f function makes our equation look like this: f(f^-1(x)) = (2x + 5 - 5) / 2. Right away we see the different steps canceling out. The +5 and the -5 in the numerator undo each other, leaving us here: f(f^-1(x)) = 2x / 2, and then the times 2 and divided by 2 undo to bring us right back to where we started - plain old x. This process actually shows us the mathematical definition of inverse functions: two functions that, when composed with each other, cancel out and get us right back to the x on the inside.

Finding Inverses

So, now that we know what inverse functions are, how might you go about finding one? Say we have the function g(x) = sqrt(2x - 3) shown here, what would the inverse of g be?

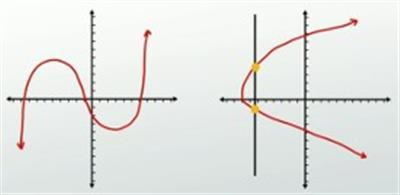
If a vertical line crosses the graph in more than one place, the relation is not a function

Well, okay, since g(x) is really just a different way of saying y, we could rewrite our function like this: y = sqrt(2x - 3). Now, relying on the knowledge that the inverse is a list of steps that are the exact opposite as the original, we can use the following trick to find any inverse function. Switching the x and the y and now solving the equation for y with inverse operations will provide us with the exact set of steps that will undo the original function.

Doing that here would mean we'd first square both sides to undo the square root, then add 3 to both sides to undo the subtraction, and finally divide by 2 to undo the multiplication. The equation we end up with, (y = (x ² + 3) / 2), is the inverse because it includes all of the inverse operations in reverse order of the original function. Therefore, g^-1(x) = (x² + 3) / 2.

The Horizontal Line Test

The last thing to cover has to do with specifics regarding what makes a function and therefore what makes its inverse. You'll need to remember that any function can only have one output for each input. One common way to test this is called the vertical line test. By tracing a vertical line across the graph, we can check to see if the relation is indeed a function. If our imaginary vertical line crosses the graph in more than one place, the relation is not a function, but if it passes across the entire graph and only ever touches the graph in one spot, it is.

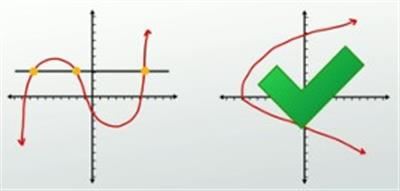
We can use a similar tactic to also test whether the inverse is a function as well, but now, similar to how we switch the x and the y to find the inverse, we switch the vertical line to a horizontal line. This means that in order to test whether a relation's inverse is a function, we use the horizontal line test instead of the vertical line test, but everything else is the same. We trace this imaginary horizontal line across the graph, looking for a place where it touches more than once. If it never does, the inverse is a function, but if it ever touches the graph in more than one spot, the inverse is not a function.

Lesson Summary

There's a lot to know about inverse functions, so let's review what we've learned. A function's inverse is another function that does the exact opposite, and we use the negative one power to express it: f ^-1(x).

If we compose a function with its inverse, the two functions essentially undo each other, leaving us right back where we started - the x. We can figure out what the inverse of a function is by swapping the x and the y and then re-solving the equation for y. And finally, to test whether or not the inverse is a true mathematical function, we can use the horizontal line test to see if our imaginary horizontal line ever touches the graph in more than one spot.

Learning Outcomes

After viewing this lesson you should be able to formulate a function's inverse and use the horizontal line test if an inverse function is a true function.

Sub Topics

GRE General: Functions Identification Notation
Inverse Functions

Inverse Functions