GRE General

Sub Topics

Domain And Range in a Function Applying Function Operations Practice Problems How to Compose Functions Add Subtract Multiply And Divide Functions Graphing Basic Functions What is a Function Basics And Key Terms Compounding Functions And Graphing Functions of Functions Inverse Functions Understanding And Graphing The Inverse Function Polynomials Functions Properties And Factoring Polynomials Functions Exponentials And Simplifying

Main Topics

Lessons and MCQs

Select Test Select Question Types

GRE General: Rational Exponents
Understanding And Graphing The Inverse Function

If you use a function to map a to b, is there a way to go back from b to a again? Learn how to find and graph inverse functions so that you can turn a into b and back into a.

Understanding And Graphing The Inverse Function

Inverse Functions

If I tell you that I have a function that maps the number of feet in some distance to the number of inches in that distance, you might tell me that the function is y=f(x) where the input x is the number of feet and the output y is the number of inches. You might even tell me that y = f(x) = 12x, because there are 12 inches in every foot. But what if I told you that I wanted a function that does the exact opposite? What if I want a function to take the number of inches as input and return the number of feet as output? Could you tell me what this function is?

Inverse functions are exactly that. If we have a function y=f(x), then the inverse function is written as y= f^-1 (x), and it does the exact opposite of the function. What happens if you put a function and its inverse into a composite function such as f^-1 (f(x))? First, we evaluate the inner function, f(x), then we're going to evaluate the outer function f^-1 (x).

Let's take a look at an example. Say we start with 4 feet. Well, our function is f(x)=12x because there are 12 inches in every foot. If we plug in 4 feet to start, then f(4) = 12 × 4 = 48 inches. Now if we take the inverse function, and the inverse function is going to be f^-1 (x) = x(1/12). So, if we take 48 inches, then our inverse function, f^-1 (48) = 48 / 12 = 4 feet. Okay, so you might be able to find f(x) and f^-1 (x) just based on your understanding of inches and feet, but how do you do it in general?

Five Steps to Inversing a Function

Write your function out in terms of x and y: y=f(x).
Swap the x and y variables: x=f(y).
Solve for y as a function of x.
Set y = f^-1 (x).
Check the composite function: f^-1 (f(x)).

Examples

Following these steps, let's say we have a function f(x)= 3(x - 1) + 2.

We're going to write this out in terms of x and y: y = 3(x - 1) + 2. Then we're going swap the x and yvariables, so we're going to write this as x = 3(y - 1) + 2. This can be a confusing step if you're not careful, but at its heart, all you're doing is putting xeverywhere you see y and putting y everywhere you see x. Then you're going to solve for y as a function of x. So I'm going to subtract 2 from both sides, x - 2 = 3(y - 1), divide both sides by 3, (x - 2) / 3 = y - 1 and add 1 to both sides and I end up with y = 1 + (x - 2)/3.

I'm going to call what's on the right-hand side my inverse function, f^-1 (x) = 1 + (x-2)/3. Finally, I'm going to check my answer, so I'm going to find f^-1 of (f(x)). To do this, I'm going to write f(x) = 3(x-1) + 2. I'm going to plug that in as input for my inverse function, so f^-1 (x) = 1 + ((3(x-1) + 2) - 2)/3. I have my input here, so I'm just going to solve and simplify for f^-1 (x) = 1 + (3(x-1))/3: f^-1 (x) = 1 + x - 1. And sure enough, f^-1 (f(x)) = x, which is exactly what we'd expect.

So what about a function like y = round(x)? Remember that round(x) just rounds our input to the nearest integer: round(4.2) = 4. However, round(4.8) = 5 and round(5.1) = 5. In this case, do you think that you can find an inverse function that can take 5 and give your either 5.1 or 4.8? No, round(x) is a function that has no inverse.

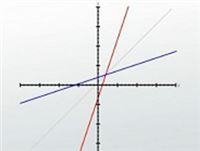
Graphing Inverse Functions

What about the function f(x) = x3 + 3x? I can write it out in terms of x and y: y = x3 + 3x. I can then swap the variables, x = y3 + 3y. I can then solve it for y - but that's not immediately obvious to me. Is there another way? Let's go back and look at an easier function, like f(x) = 3x - 6. I end up with a graph that looks like this, a simple line. Now I'm going to graph the inverse, which is f^-1 (x) = (x + 6)/3. So the inverse is this blue line; it looks a lot like the original function, except it's mirrored. And it's actually mirrored over the 45-degree angle, which is the x=y line. If I could fold this paper in half, then I'd see that the function and its inverse become the same line. I can use this on much more complex functions too. Say I was looking at a function like this. If I draw the 45-degree line and mirror it, then I can get a pretty good idea of what that inverse function looks like.