Understanding the Five Exponent Properties
We are going to talk about five exponent properties. You can think about them as the order of operations for exponents. Just like the order of operations, you need to memorize these operations to be successful. The five exponent properties are:
The Quotient of Powers property
- Product of Powers
- Power to a Power
- Quotient of Powers
- Power of a Product
- Power of a Quotient
Let's look at the first one.
Product of Powers
Here's the formula: (x^a)(x^b) = x^(a + b). When you multiply exponentials with the same base (notice that xand x are the same base), add their exponents (or powers).
Let me show you how that works. Let's say I have (x^2)(x^3). Well, x^2 is x times x, and x^3 is x times x times x. When we add all those xs up, we get x^5, which is the same thing as adding 3 + 2.
Power to a Power
The Power of a Product property
We can see from the formula we have (x^a)^b. When you have a power to a power, you multiply the exponents (or powers). Let me show you how this one works.
If I have (x^2)^4, which would be x^2 multiplied four times, or x^2 times x^2 times x^2 times x^2. Once again, we add all the exponents and get x^8, and x^8 is the same as x^(2 ×4), which is 8. Not too bad, right?
Quotient of Powers
Remember, 'quotient' means 'division'.' The formula says (x^a) / (x^b) = x^(a - b). Basically, when you divide exponentials with the same base, you subtract the exponent (or powers).
Let me show you how this one works. Let's say I had (x^4) / (x^3). In the top (or numerator), we have x times x times x times x. In the bottom (or denominator), we have x times x times x. Hopefully, you remember that xdivided by x is 1, so the xs cancel. So, x divided by x is 1, x divided by x is 1, and x divided by x is 1. So, when we cancel them, what are we left with? That's right: x^1, or just x. So (x^4) / (x^3) is just x^(4 - 3), which is x^1.
kkk
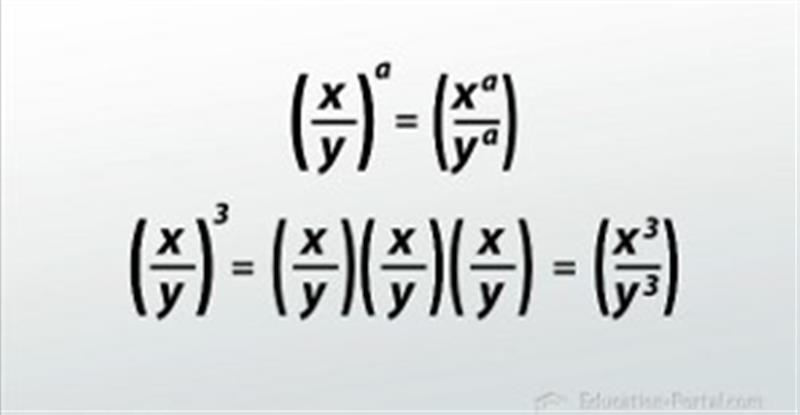
The Power of a Quotient Property