Set Review
Before we get into Venn diagrams, let's review sets. A set is a collection of elements. An element is a collection of anything - numbers, letters, words, objects. Using math symbols, the symbol below means element.
Element = ∊ -
Mathematical symbol for element
A subset is a special, funny set. If every element in one set is included in another set, they are called subsets. Using math symbols, the symbol below means subset.
Subset = ⊆ -
Mathematical symbol for subset
Let's say our universe is the things, or elements, in my apartment. So, our universal set U = {fork, spoon, knife, spatula, whisk, plate, cup, napkin, tablecloth, television, couch}.
Let set K be a list of utensils in my kitchen. K = {fork, spoon, knife, spatula, whisk}.
Let set T be a list of things, or elements, on my table. T= {plate, fork, knife, cup, napkin, tablecloth}.
So, we can say that a fork is an element of K. Using math symbols, we would write:
fork ∊ K
fork : “is an element of”K
or
fork “belongs to “ K
Fork is an element of K, using math symbols.
This is read, 'Fork is an element of K,' or, 'Fork belongs to K.' That makes sense because the fork belongs in the kitchen.
Set Operations
Let's use sets K and T to review set operations.
Union
Union is when two or more sets are united, or added together.
K union T = all of the elements of set K or all of the elements in set T, and that would equal {fork, spoon, knife, spatula, whisk, plate, cup, napkin, tablecloth}.
The 'or' tells us that it is any object in set K, the kitchen, or set T, on the table.
Intersection
- Intersection is when two or more sets intersect, or are common objects, in sets.
- K intersects T = all of the numbers in set K and set T, and that equals {fork, knife}.
- The 'and' tells us that it is in the kitchen and on the table at the same time.
Complement
Complement is when a set is subtracted or not included in the set.
K' = everything not in the kitchen, not in set K, and that equals {plate, cup, napkin, tablecloth, television, couch}.
Venn Diagram
A Venn diagram can show us the sets and operations nicely in picture form. Let's look at union, intersection and complement using a Venn diagram. We're going to continue using set K and set T. Below is what a Venn diagram showing the sets K and T looks like:
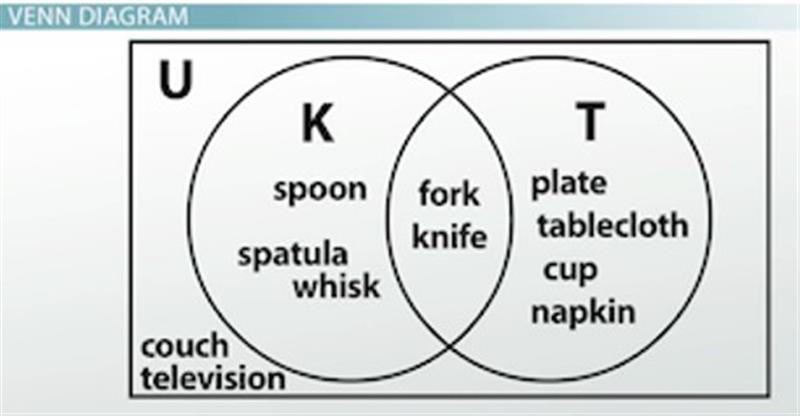
Venn diagram of sets K and T
Let's examine how the Venn diagram is created.
There's a circle for each set - one circle for set K and another circle for set T. You can see that we labeled the circles so we don't get them mixed up. We only have two circles because we only have two sets, but you will also see Venn diagrams with more than two circles.
The circles intersect because there are objects, or elements, in each set that are the same. We would say K intersects T = {fork, knife}.
I hope you notice that television and couch are listed in the universal set, but not found in set K or set T. Even though we didn't use it in a set, we still need to show it. In all cases where this happens, we list it outside the circles but within the box or universe.
Union
K union T = {fork, spoon, knife, spatula, whisk, plate, cup, napkin, tablecloth}.
To show union in a Venn diagram, we highlight the circle K and circle T:
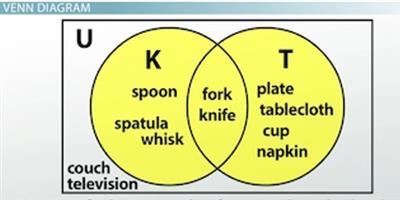
K U T = {fork, spoon, knife, spatula, whisk , plate, cup, napkin, table cloth}
Highlighting sets in a Venn diagram shows union.