Translating Horizontally and Vertically
We'll get to some of these other transformations in a later lesson, but in this lesson we're going to focus on two of the most common transformations you see on absolute value graphs, and those are the shift up/down and left/right. Any transformation that just moves the graph to a new place, but doesn't actually change the size or shape of it is called a translation.
The shift left/right is accomplished by adding or subtracting to the x within the absolute value. Take the example y=|x-3|. The vertex, or the bottom of the V, is the lowest point of the absolute value, and the way we get the lowest point is have the absolute value be 0, because it can't ever be negative, so the lowest it's going to get is at zero. So before the vertex was at (0,0), but now the only way I can make the absolute value 0 is by substituting in x=3. Then I do 3-3 and I get 0, and so my vertex has now been shifted over to the point (3,0), which means my whole V, my whole graph gets shifted over there, so we end up with the following graph.
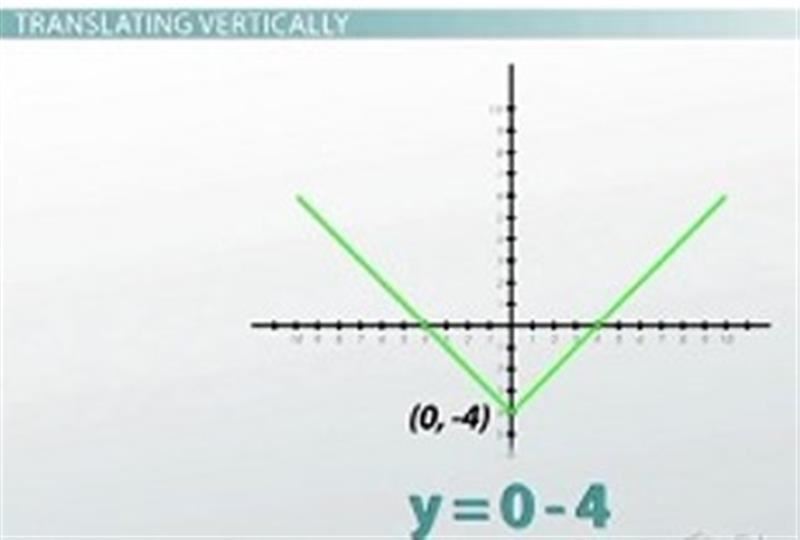
Subtracting on the outside of the absolute value moves the entire graph downward
Therefore, any number being subtracted on the inside of the absolute value tells us how much shift the graph to the right, which means when you add a number on the inside of the absolute value, you need to shift the graph to the left. For example, y=|x+4| would be over here. This one is easy to make mistakes on because you have to do the opposite of what you'd expect. But I always remind myself by asking 'what do I need to substitute in to make it 0,' and that's always going to be the opposite of the operation going on on the inside.
The shift up/down is accomplished by adding or subtracting on the outside of the absolute value. Take the example y=|x|-4. Again the vertex is the lowest point of the graph, and the vertex happens when I take the absolute value of 0, and in this example I'm still going to get the absolute value of 0 just by substituting in 0, but after I do that I still have to subtract 4, so the whole graph gets dragged down 4, and my vertex ends up at (0,-4). This means that subtracting on the outside of the absolute value pulls the whole graph down, which means that adding on the outside of the absolute value pushes the whole graph up. For example, y=|x|+1 would look like this graph here.
This one is normal in the sense that the plus moves it up and the minus moves it down, so it's kind of what you'd expect, whereas the left/right translation is a little bit backwards, so you've got to try to keep those two things organized.
Graphing a Standard Absolute Value Graph
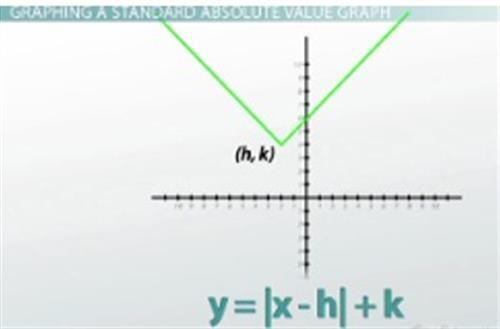
y= |x-h|+k is the general form of an absolute value equation
We can combine both of these translations into one problem, and graph things like y=|x+2|+4 by taking our V with vertex at (0,0) and moving it over 2 to the left (because of the +2 on the inside), and up 4 (because of the +4 on the outside) and ending up with an absolute value graph that has a vertex at (-2,4). Because the vertex has coordinates at the values that are being added/subtracted to the equation, the general form of an absolute value equation is y=|x-h|+k where vertex=(h,k). Notice that the h is being subtracted on the inside of the absolute value in the general form, which means that it does the opposite of what you might expect.
Lesson Summary
- Absolute value graphs look like the letter V - or the absolute coolest guitar ever, the Gibson Flying V - because where the line would normally turn negative, it the absolute value bounces back up to the positives.
- Transformations change how the graph looks, and the specific transformation that moves the graph to a different place is called a translation.
- The general form equation y=|x-h|+k gives us a graph with a vertex at (h,k) because the number on the inside of the absolute value shifts the graph left/right and the number on the outside shifts it up/down.